DSP Blockset

Least Squares Polynomial Fit

Compute the coefficients of the polynomial that best fits the input data in a least-squares sense.

Library

Math Functions / Polynomial Functions

Description

The Least Squares Polynomial Fit block computes the coefficients of the nth order polynomial that best fits the input data in the least-squares sense, where n is specified by the Polynomial order parameter. A distinct set of n+1 coefficients is computed for each column of the M-by-N input, u.

For a given input column, the block computes the set of coefficients, c₁, c₂, ..., cn₊₁, that minimizes the quantity

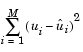
where ui is the ith element in the input column, and

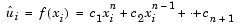
The values of the independent variable, x₁, x₂, ..., x_M, are specified as a length-M vector by the Control points parameter. The same M control points are used for all N polynomial fits, and can be equally or unequally spaced. The equivalent MATLAB code is shown below.

c = polyfit(x,u,n)       % Equivalent MATLAB code

Inputs can be frame-based or sample-based. For convenience, a length-M 1-D vector input is treated as an M-by-1 matrix.

Each column of the (n+1)-by-N output matrix, c, represents a set of n+1 coefficients describing the best-fit polynomial for the corresponding column of the input. The coefficients in each column are arranged in order of descending exponents, c₁, c₂, ..., cn₊₁. The output is always sample-based.

Example

In the model below, the Polynomial Evaluation block uses the second-order polynomial

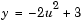
to generate four values of dependent variable y from four values of independent variable u, received at the top port. The polynomial coefficients are supplied in the vector [-2 0 3] at the bottom port. Note that the coefficient of the first-order term is zero.

The Control points parameter of the Least Squares Polynomial Fit block is configured with the same four values of independent variable u that are used as input to the Polynomial Evaluation block, [1 2 3 4]. The Least Squares Polynomial Fit block uses these values together with the input values of dependent variable y to reconstruct the original polynomial coefficients.

Dialog Box

Control points

The values of the independent variable to which the data in each input column correspond. For an M-by-N input, this parameter must be a length-M vector.

Polynomial order

The order, n, of the polynomial to be used in constructing the best fit. The number of coefficients is n+1.

See Also

Detrend	DSP Blockset
Polynomial Evaluation	DSP Blockset
Polynomial Stability Test	DSP Blockset
polyfit	MATLAB

Least Squares FIR Filter Design

Levinson-Durbin