DSP Blockset

Filter Structures

Any realizable filter can be represented in the time domain by a difference equation of the form

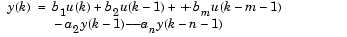
where y(k) and u(k) are, respectively, the output and input at the current time step, y(k-1) and u(k-1) are the output and input at the previous time step, and so on. The values b₁, b₂, ..., bm, and a₂, ..., an are the filter coefficients, or taps.

Every realizable filter is therefore fundamentally a collection of multiplications, additions, and delays. The order in which these assorted operations are implemented in practice determines the filter structure (also known as the filter realization, architecture, or implementation). Implementations may differ from each other in terms of speed, memory requirements, delay, and quantization error. See Linear System Models in the Signal Processing Toolbox documentation for more information about common filter structures.

The Filter Structures library provides a number of blocks for filter implementation:

• Analog Filter Design
• Biquadratic Filter
• Direct-Form II Transpose Filter
• Overlap-Add FFT Filter
• Overlap-Save FFT Filter
• Time-Varying Direct-Form II Transpose Filter
• Time-Varying Lattice Filter

Additionally, the library includes the Filter Realization Wizard for creating a variety of custom designs.

The DSP Blockset provides a number demos that make use of the filter structure blocks:

• Frequency Domain Filtering (olapfilt)
• LPC Analysis and Synthesis of Speech (dsplpc)
• Sample Rate Conversion (dspsrcnv)

Example: Least Squares Multiband Filter

Multirate Filters