DSP Blockset

Multiband Discrete-Time FIR Filters.   The normalized cutoff frequencies for a multiband filter are illustrated in the next figure. Multiband filters are constructed in the same way as bandpass or bandstop filters, except that a vector of cutoff frequencies, fn, is specified (instead of just an upper and lower cutoff frequency pair). In the figure, the normalized cutoff frequencies are

fn = [0.2 0.5 0.7]

For an input signal sampled at 1 kHz, these would be equivalent to cutoff frequencies of 100 Hz, 250 Hz, and 350 Hz, respectively. The right plot shows a zoomed view of the third transition region, defined by cutoff frequency fn(3).

The equivalent MATLAB code for this filter design is

b = fir1(41,[0.2 0.5 0.7],'dc-1')

and the filter can be designed in the Digital FIR Filter Design block by making the following selections in the dialog box:

• Filter type = Multiband
• Order = 41
• Cutoff frequency vector = [0.2 0.5 0.7]
• Gain in the first band = 1

A multiband filter response alternates between passband (gain 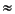 1) and stopband (gain  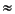0) for however many bands are specified in the cutoff frequency vector. The Gain in the first band indicates whether the band pattern begins with a stopband or passband: 0 indicates an initial stopband, and 1 indicates an initial passband. In general, if the first (leftmost) band is a passband, as shown above, the frequency vector describes the response as follows:

fn(1)	=	first passband-to-stopband cutoff frequency
fn(2)	=	first stopband-to-passband cutoff frequency
fn(3)	=	second passband-to-stopband cutoff frequency
fn(4)	=	second stopband-to-passband cutoff frequency

If the first (leftmost) band is a stopband, as shown below, the frequency vector describes the response as follows:

fn(1)	=	first stopband-to-passband cutoff frequency
fn(2)	=	first passband-to-stopband cutoff frequency
fn(3)	=	second stopband-to-passband cutoff frequency
fn(4)	=	second passband-to-stopband cutoff frequency

The equivalent MATLAB code for an initial-stopband response is

b = fir1(41,[0.2 0.5 0.7],'dc-0')

Whenever the last (right-most) band is a passband, as it is above, the filter order must be even (so that the filter is Type I). MATLAB therefore automatically increases the filter order to 42 for this example.

Bandpass and Bandstop Discrete-Time FIR Filters

Arbitrary Shape Discrete-Time FIR Filters