DSP Blockset

Cholesky Solver

Solve the equation SX=B for X when S is a square Hermitian positive definite matrix.

Library

Math Functions / Matrices and Linear Algebra / Linear System Solvers

Description

The Cholesky Solver block solves the linear system SX=B by applying Cholesky factorization to input matrix at the S port, which must be square (M-by-M) and Hermitian positive definite. Only the diagonal and upper triangle of the matrix are used, and any imaginary component of the diagonal entries is disregarded. The input to the B port is the right-hand side M-by-N matrix, B. The output is the unique solution of the equations, M-by-N matrix X, and is always sample-based.

When the input is not positive definite, the block reacts with the behavior specified by the Non-positive definite input parameter. The following options are available:

• Ignore - Proceed with the computation and do not issue an alert. The output is not a valid solution.
• Warning - Proceed with the computation and display a warning message in the MATLAB command window. The output is not a valid solution.
• Error - Display an error dialog box and terminate the simulation.

A length-M vector input for right-hand side B is treated as an M-by-1 matrix.

Algorithm

Cholesky factorization uniquely factors the Hermitian positive definite input matrix S as

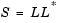
where L is a lower triangular square matrix with positive diagonal elements.

The equation SX=B then becomes

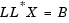
which is solved for X by making the substitution Y = L^*X, and solving the following two triangular systems by forward and backward substitution, respectively.

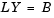
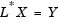
Dialog Box

Non-positive definite input

Response to non-positive definite matrix inputs. Tunable.

See Also

Autocorrelation LPC	DSP Blockset
Cholesky Factorization	DSP Blockset
Cholesky Inverse	DSP Blockset
LDL Solver	DSP Blockset
LU Solver	DSP Blockset
QR Solver	DSP Blockset
chol	MATLAB

See Solving Linear Systems for related information.

Cholesky Inverse

Complex Cepstrum