Creating and Manipulating Models

Specifying Delays in Discrete-Time Models

You can also use the ioDelay, InputDelay, and OutputDelay properties to specify delays in discrete-time LTI models. You specify time delays in discrete-time models with integer multiples of the sampling period. The integer k you supply for the time delay of a discrete-time model specifies a time delay of k sampling periods. Such a delay contributes a factor 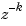to the transfer function.

For example,

h = tf(1,[1 0.5 0.2],0.1,'inputdelay',3)

produces the discrete-time transfer function

Transfer function:
                 1
z^(-3) * -----------------
         z^2 + 0.5 z + 0.2
 
Sampling time: 0.1

Notice the z^(-3) factor reflecting the three-sampling-period delay on the input.

Mapping Discrete-Time Delays to Poles at the Origin

Since discrete-time delays are equivalent to additional poles at 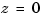, they can be easily absorbed into the transfer function denominator or the state-space equations. For example, the transfer function of the delayed integrator

is

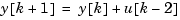
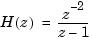
You can specify this model either as the first-order transfer function 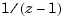with a delay of two sampling periods on the input

Ts = 1;    % sampling period
H1 = tf(1,[1 -1],Ts,'inputdelay',2)

or directly as a third-order transfer function:

H2 = tf(1,[1 -1 0 0],Ts)    % 1/(z^3-z^2)

While these two models are mathematically equivalent, H1 is a more efficient representation both in terms of storage and subsequent computations.

When necessary, you can map all discrete-time delays to poles at the origin using the command delay2z. For example,

H2 = delay2z(H1)

absorbs the input delay in H1 into the transfer function denominator to produce the third-order transfer function

Transfer function:
    1
---------
z^3 - z^2
 
Sampling time: 1

Note that

H2.inputdelay

now returns 0 (zero).

Specifying Delays on the Inputs or Outputs

Retrieving Information About Delays