

| MATLAB Function Reference |   |
Syntax
slice(V,sx,sy,sz)
slice(X,Y,Z,V,sx,sy,sz)
slice(V,XI,YI,ZI)
slice(X,Y,Z,V,XI,YI,ZI)
slice(...,'method')
h = slice(...)
Description
slice displays orthogonal slice planes through volumetric data.
slice(V,sx,sy,sz)
draws slices along the x, y, z directions in the volume V at the points in the vectors sx, sy, and sz. V is an m-by-n-by-p volume array containing data values at the default location X = 1:n, Y = 1:m, Z = 1:p. Each element in the vectors sx, sy, and sz defines a slice plane in the x-, y-, or z-axis direction.
slice(X,Y,Z,V,sx,sy,sz)
draws slices of the volume V. X, Y, and Z are three-dimensional arrays specifying the coordinates for V. X, Y, and Z must be monotonic and orthogonally spaced (as if produced by the function meshgrid). The color at each point is determined by 3-D interpolation into the volume V.
slice(V,XI,YI,ZI)
draws data in the volume V for the slices defined by XI, YI, and ZI. XI, YI, and ZI are matrices that define a surface, and the volume is evaluated at the surface points. XI, YI, and ZI must all be the same size.
slice(X,Y,Z,V,XI,YI,ZI)
draws slices through the volume V along the surface defined by the arrays XI, YI, ZI.
slice(...,' specifies the interpolation method. method')
'method' is 'linear', 'cubic', or 'nearest'.
linear specifies trilinear interpolation (the default).cubic specifies tricubic interpolation.nearest specifies nearest neighbor interpolation. h = slice(...)
returns a vector of handles to surface graphics objects.
Remarks
The color drawn at each point is determined by interpolation into the volume V.
Examples
over the range -2 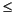 x
x 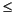 2, -2
2, -2 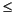 y
y 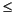 2, - 2
2, - 2 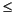 z
z 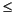 2:
2:
[x,y,z] =meshgrid(-2:.2:2,-2:.25:2,-2:.16:2); v = x.*exp(-x.^2-y.^2-z.^2); xslice = [-1.2,.8,2]; yslice = 2; zslice = [-2,0];slice(x,y,z,v,xslice,yslice,zslice) colormap hsv
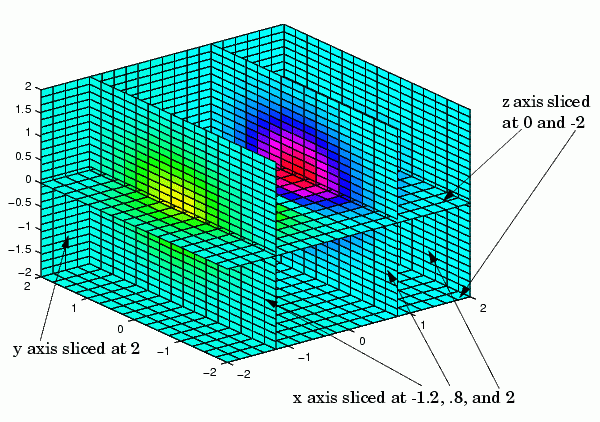
Slicing At Arbitrary Angles
You can also create slices that are oriented in arbitrary planes. To do this,
surf, linspace).rotate).XData, YData, and ZData of the surface (get).For example, these statements slice the volume in the first example with a rotated plane. Placing these commands within a for loop "passes" the plane through the volume along the z-axis.
for i = -2:.5:2
hsp = surf(linspace(-2,2,20),linspace(-2,2,20),zeros(20)+i);
rotate(hsp,[1,-1,1],30)
xd = get(hsp,'XData');
yd = get(hsp,'YData');
zd = get(hsp,'ZData');
delete(hsp)
slice(x,y,z,v,[-2,2],2,-2) % Draw some volume boundaries
hold on
slice(x,y,z,v,xd,yd,zd)
hold off
axis tight
view(-5,10)
drawnow
end
The following picture illustrates three positions of the same slice surface as it passes through the volume.
Slicing with a Nonplanar Surface
You can slice the volume with any surface. This example probes the volume created in the previous example by passing a spherical slice surface through the volume.
[xsp,ysp,zsp] = sphere;
slice(x,y,z,v,[-2,2],2,-2) % Draw some volume boundaries
for i = -3:.2:3
hsp = surface(xsp+i,ysp,zsp);
rotate(hsp,[1 0 0],90)
xd = get(hsp,'XData');
yd = get(hsp,'YData');
zd = get(hsp,'ZData');
delete(hsp)
hold on
hslicer = slice(x,y,z,v,xd,yd,zd);
axis tight
xlim([-3,3])
view(-10,35)
drawnow
delete(hslicer)
hold off
end
The following picture illustrates three positions of the spherical slice surface as it passes through the volume.
See Also
interp3,meshgrid
 | size (serial) | smooth3 |  |