

| MATLAB Function Reference |   |
Convert between partial fraction expansion and polynomial coefficients
Syntax
[r,p,k] = residue(b,a) [b,a] = residue(r,p,k)
Description
The residue function converts a quotient of polynomials to pole-residue representation, and back again.
[r,p,k] = residue(b,a)
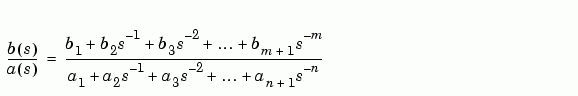
[b,a] = residue(r,p,k)
b and a.
Definition
If there are no multiple roots, then:
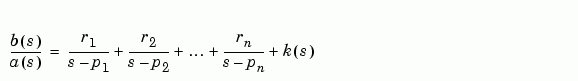
n = length(a)-1 = length(r) = length(p)
The direct term coefficient vector is empty if length(b) < length(a); otherwise
length(k) = length(b)-length(a)+1
If p(j) = ... = p(j+m-1) is a pole of multiplicity m, then the expansion includes terms of the form

Arguments
b,a |
Vectors that specify the coefficients of the polynomials in descending powers of s |
r |
Column vector of residues |
p |
Column vector of poles |
k |
Row vector of direct terms |
Algorithm
The residue function is an M-file. It first obtains the poles with roots. Next, if the fraction is nonproper, the direct term k is found using deconv, which performs polynomial long division. Finally, the residues are determined by evaluating the polynomial with individual roots removed. For repeated roots, the M-file resi2 computes the residues at the repeated root locations.
Limitations
Numerically, the partial fraction expansion of a ratio of polynomials represents an ill-posed problem. If the denominator polynomial, a(s), is near a polynomial with multiple roots, then small changes in the data, including roundoff errors, can make arbitrarily large changes in the resulting poles and residues. Problem formulations making use of state-space or zero-pole representations are preferable.
See Also
References
[1] Oppenheim, A.V. and R.W. Schafer, Digital Signal Processing, Prentice-Hall, 1975, p. 56.
 | reshape | return |  |