

| MATLAB Function Reference |   |
Syntax
P=legendre(n,X) S = legendre(n,X,'sch')
Definition
The Legendre functions are defined by:
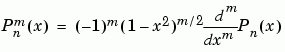
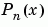
is the Legendre polynomial of degree n:
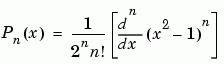
The Schmidt seminormalized associated Legendre functions are related to the nonnormalized associated Legendre functions
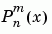 by:
by:
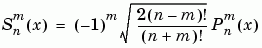
Description
P = legendre(n,X)
computes the associated Legendre functions of degree n and order m = 0,1,...,n, evaluated at X. Argument n must be a scalar integer less than 256, and X must contain real values in the domain -1 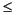 x
x 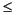 1.
1.
The returned array P has one more dimension than X, and each element P(m+1,d1,d2...) contains the associated Legendre function of degree n and order m evaluated at X(d1,d2...).
If X is a vector, then P is a matrix of the form:
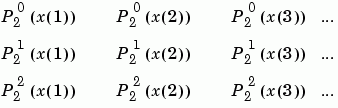
S = legendre(...,'sch')
computes the Schmidt seminormalized associated Legendre functions 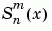 .
.
Examples
The statement legendre(2,0:0.1:0.2) returns the matrix:
| x = 0 |
x = 0.1 |
x = 0.2 |
|
| m = 0 |
-0.5000 |
-0.4850 |
-0.4400 |
| m = 1 |
0 |
-0.2985 |
-0.5879 |
| m = 2 |
3.0000 |
2.9700 |
2.8800 |
Note that this matrix is of the form shown at the bottom of the previous page.
X = rand(2,4,5); N = 2; P = legendre(N,X)
Then size(P) is 3-by-2-by-4-by-5, and P(:,1,2,3) is the same as legendre(n,X(1,2,3)).
 | legend | length |  |