Mathematics

Eigenvalues and Singular Values

Two functions are available which compute a few specified eigenvalues or singular values. svds is based on eigs which uses ARPACK [6].

Functions to Compute a Few Eigenvalues or Singular Values  

Function	Description
eigs	Few eigenvalues
svds	Few singular values

These functions are most frequently used with sparse matrices, but they can be used with full matrices or even with linear operators defined by M-files.

The statement

[V,lambda] = eigs(A,k,sigma)

finds the k eigenvalues and corresponding eigenvectors of the matrix A which are nearest the "shift" sigma. If sigma is omitted, the eigenvalues largest in magnitude are found. If sigma is zero, the eigenvalues smallest in magnitude are found. A second matrix, B, may be included for the generalized eigenvalue problem

The statement

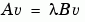
[U,S,V] = svds(A,k)

finds the k largest singular values of A and

[U,S,V] = svds(A,k,0)

finds the k smallest singular values.

For example, the statements

L = numgrid('L',65);
A = delsq(L);

set up the five-point Laplacian difference operator on a 65-by-65 grid in an L-shaped, two-dimensional domain. The statements

size(A)
nnz(A)

show that A is a matrix of order 2945 with 14,473 nonzero elements.

The statement

[v,d] = eigs(A,1,0);

computes the smallest eigenvalue and eigenvector. Finally,

L(L>0) = full(v(L(L>0)));
x = -1:1/32:1;
contour(x,x,L,15)
axis square

distributes the components of the eigenvector over the appropriate grid points and produces a contour plot of the result.

The numerical techniques used in eigs and svds are described in [6].

Simultaneous Linear Equations

Selected Bibliography