

| Mathematics |   |
Multiple Regression
If y is a function of more than one independent variable, the matrix equations that express the relationships among the variables can be expanded to accommodate the additional data.
Suppose we measure a quantity y for several values of parameters 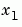 and
and 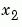 . The observations are entered as
. The observations are entered as
x1 = [.2 .5 .6 .8 1.0 1.1]'; x2 = [.1 .3 .4 .9 1.1 1.4]'; y = [.17 .26 .28 .23 .27 .24]';
A multivariate model of the data is
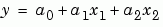
Multiple regression solves for unknown coefficients 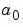 ,
,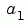 , and
, and 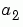 , by performing a least squares fit. Construct and solve the set of simultaneous equations by forming the regression matrix,
, by performing a least squares fit. Construct and solve the set of simultaneous equations by forming the regression matrix, X, and solving for the coefficients using the backslash operator.
X = [ones(size(x1)) x1 x2];
a = X\y
a =
0.1018
0.4844
-0.2847
The least squares fit model of the data is
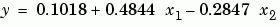
To validate the model, find the maximum of the absolute value of the deviation of the data from the model.
Y = X*a;
MaxErr = max(abs(Y - y))
MaxErr =
0.0038
This is sufficiently small to be confident the model reasonably fits the data.
 | Linear-in-the-Parameters Regression | Case Study: Curve Fitting |  |