Mathematics

Overdetermined Systems

Overdetermined systems of simultaneous linear equations are often encountered in various kinds of curve fitting to experimental data. Here is a hypothetical example. A quantity y is measured at several different values of time, t, to produce the following observations.

t	y
0.0	0.82
0.3	0.72
0.8	0.63
1.1	0.60
1.6	0.55
2.3	0.50

This data can be entered into MATLAB with the statements

t = [0 .3 .8 1.1 1.6 2.3]';
y = [.82 .72 .63 .60 .55 .50]';

The data can be modeled with a decaying exponential function.

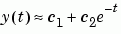
This equation says that the vector y should be approximated by a linear combination of two other vectors, one the constant vector containing all ones and the other the vector with components e^-t. The unknown coefficients, c₁ and c₂, can be computed by doing a least squares fit, which minimizes the sum of the squares of the deviations of the data from the model. There are six equations in two unknowns, represented by the 6-by-2 matrix.

E = [ones(size(t)) exp(-t)]

E =
      1.0000    1.0000
      1.0000    0.7408
      1.0000    0.4493
      1.0000    0.3329
      1.0000    0.2019
      1.0000    0.1003

The least squares solution is found with the backslash operator.

c = E\y

c =
      0.4760
      0.3413      

In other words, the least squares fit to the data is

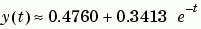
The following statements evaluate the model at regularly spaced increments in t, and then plot the result, together with the original data.

T = (0:0.1:2.5)';
Y = [ones(size(T)) exp(-T)]*c;
plot(T,Y,'-',t,y,'o')

You can see that E*c is not exactly equal to y, but that the difference might well be less than measurement errors in the original data.

A rectangular matrix A is rank deficient if it does not have linearly independent columns. If A is rank deficient, the least squares solution to AX = B is not unique. The backslash operator, A\B, issues a warning if A is rank deficient and produces a basic solution that has as few nonzero elements as possible.

Square Systems

Underdetermined Systems