Getting Started

Multidimensional Arrays

Multidimensional arrays in MATLAB are arrays with more than two subscripts. They can be created by calling zeros, ones, rand, or randn with more than two arguments. For example,

R = randn(3,4,5);

creates a 3-by-4-by-5 array with a total of 3x4x5 = 60 normally distributed random elements.

A three-dimensional array might represent three-dimensional physical data, say the temperature in a room, sampled on a rectangular grid. Or, it might represent a sequence of matrices, A^(k), or samples of a time-dependent matrix, A(t). In these latter cases, the (i, j)th element of the kth matrix, or the t_kth matrix, is denoted by A(i,j,k).

MATLAB's and Dürer's versions of the magic square of order 4 differ by an interchange of two columns. Many different magic squares can be generated by interchanging columns. The statement

p = perms(1:4);

generates the 4! = 24 permutations of 1:4. The kth permutation is the row vector, p(k,:). Then

A = magic(4);
M = zeros(4,4,24);
for k = 1:24
   M(:,:,k) = A(:,p(k,:));
end

stores the sequence of 24 magic squares in a three-dimensional array, M. The size of M is

size(M)

ans =
     4     4    24

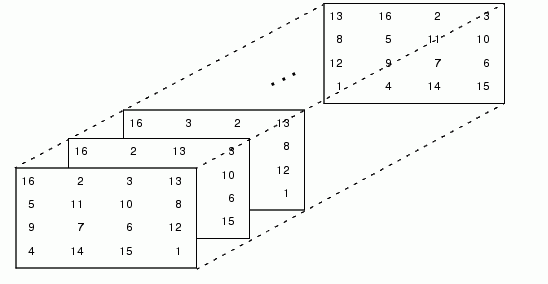
It turns out that the third matrix in the sequence is Dürer's.

M(:,:,3)

ans =
    16     3     2    13
     5    10    11     8
     9     6     7    12
     4    15    14     1

The statement

sum(M,d)

computes sums by varying the dth subscript. So

sum(M,1)

is a 1-by-4-by-24 array containing 24 copies of the row vector

34    34    34    34

and

sum(M,2)

is a 4-by-1-by-24 array containing 24 copies of the column vector

34    
34    
34    
34

Finally,

S = sum(M,3)

adds the 24 matrices in the sequence. The result has size 4-by-4-by-1, so it looks like a 4-by-4 array.

S =
   204   204   204   204
   204   204   204   204
   204   204   204   204
   204   204   204   204

Other Data Structures

Cell Arrays