Wavelet analysis example
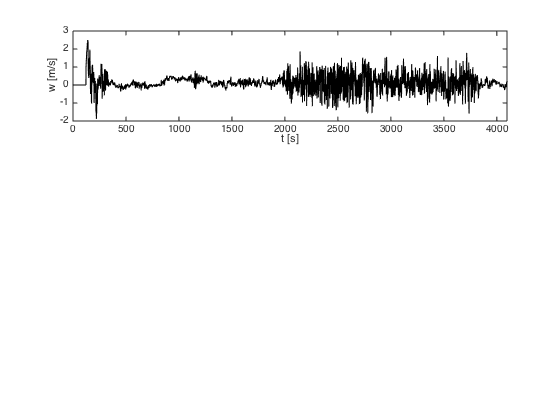
Haar wavelet analysis of a nonstationary dataset of aircraft-measured vertical velocity measured each second while the plane moved up and down through the lower layers of the atmosphere.
Contents
Load, subset and plot data
clear all load w_VOCALSRF03; whos N= 4096; w = w(1:N); % Subset to first 4096 samples for simplicity figure(1) clf subplot(3,1,1) plot(w,'k') % Note that data is quite nonstationary xlim([0 N]) xlabel('t [s]') ylabel('w [m/s]')
Name Size Bytes Class Attributes w 30241x1 241928 double
Plot level-1 Haar transform of s
[cA1,cD1] = dwt(w,'db1'); % Single-level Haar (db1) wavelet transform A1 = upcoef('a',cA1,'db1',1,N); % Average time series D1 = upcoef('d',cD1,'db1',1,N); % Detail time series subplot(3,1,2) plot(1:N/2,cA1,'b',(N/2+1):N,cD1,'r') xlim([0 N]) legend('a^1','d^1') ylabel('1-level Haar DWT')

Plot partitioning of signal into average and detail components.
subplot(3,1,3) plot(1:N,A1,'b',1:N,D1,'r') xlim([0 N]) legend('A^1','D^1') ylabel('Partitioning of signal')

3-level Haar transform
figure(2) clf [C,L] = wavedec(w,3,'db1'); A3 = wrcoef('a',C,L,'db1',3); D1 = wrcoef('d',C,L,'db1',1); D2 = wrcoef('d',C,L,'db1',2); D3 = wrcoef('d',C,L,'db1',3) ; % Plot level-3 Haar transform subplot(3,1,1) plot(1:N/8,C(1:N/8),'b',(N/8+1):(N/4),C((N/8+1):(N/4)),'c',... (N/4+1):(N/2),C((N/4+1):(N/2)),'m',... (N/2+1):N,C((N/2+1):N),'r') xlim([0 N]) ylabel('3-level Haar DWT') legend('a^3','d^3','d^2','d^1') % Plot signal and the 3rd level averaged signal subplot(3,1,2) plot(1:N,w,'k',1:N,A3,'b') xlim([0 N]) legend('signal','A^3') % Plot the three detail components of signal subplot(3,1,3) yoff = 2; plot(1:N,D1,'r',1:N,D2+yoff,'m',1:N,D3+2*yoff,'c') xlim([0 N]) ylim([-yoff,3*yoff]) legend('D1','D2','D3')

Wavelet power averaged over 64-s windows
Nw = 64; nwins = N/Nw; tw = Nw*((1:nwins) - 0.5); % Time at window centers A3pow = mean(reshape(A3.^2,Nw,nwins)); D3pow = mean(reshape(D3.^2,Nw,nwins)); D2pow = mean(reshape(D2.^2,Nw,nwins)); D1pow = mean(reshape(D1.^2,Nw,nwins)); figure(3) clf subplot(3,1,1) plot(tw,D1pow,'r.',... tw,D1pow+D2pow,'m.',... tw,D1pow+D2pow+D3pow,'c.',... tw,D1pow+D2pow+D3pow+A3pow,'b.') xlim([0 N]) xlabel('t [s]') ylabel('var(w) [m^2s^{-2}]') legend('D1','+D2','+D3','+A3')

CWT example
scale = 2.^((1:40)/4); W = cwt(w,scale,'haar'); figure(4) clf image(1:N,(1:40)/4,W,'CDataMapping','scaled') title('CWT of w - vertical axis is log2(scale)') xlabel('t [s]') ylabel('log2(scale)') axis xy
