Climate and Climate Change
Planetary Energy Balance
How do we calculate the Earth's effective temperature?
Use the idea of an energy balance: What comes in = what goes out
1) How much energy is
received by the earth?
Solar radiation incident on the Earth's
disk (1370 Watts per square meter) --comparable to energy incident a flat,
horizontal surface when the sun is directly overhead on a clear day.
We need to multiply the incoming solar
energy by the factor 1/4--the
ratio of the area of the earth's disk
(pi R2) to the Earth's surface area (4 pi R2)-- You
can think of this as spreading out the incident solar radiation uniformly
over the earth's surface (the night side of the earth as well as the day
side) 1370 / 4 = 342.5 watts per square meter.
Then we need to multiply by the factor 0.70, which takes into account the fact that 30% of the incident solar radiation is reflected back to space by clouds, snow and ice, the light colored sands of the deserts, and even just a bit from the daisies. 342.5 x 0.7 = 239.7 watts per square meter. The 0.70 is equivalent to the factor (1-A) in the formula in the text.
Energy flux absorbed by the Earth = 1370 x (1-0.3) / 4 = 239.7 W/m2
2) How much energy does
the Earth have to get rid of?
239.7 watts per square meter.
3) How does the Earth
get rid of that energy?
By emitting radiation. That's the only
way an isolated planet like the Earth can get rid of energy. Most of the
energy emitted by the Earth and the other planets is in the infrared part
of the electromagnetic spectrum. (They're not warm enough to emit an appreciable
amount of visible radiation).
What does the emitted radiation tell us about the Earth's temperature? We can calculate the temperature a black body would have to have in order to emit the same amount of radiation as the Earth. This is called the effective radiating temperature. It's the temperature that would be measured by an infrared thermometer (radiometer) in outer space, pointed at the Earth.
4) How do we calculate
the effective temperature?
From the Stefan-Boltzmann Law which says
that the emitted radiation is equal to a constant times the effective radiating
temperature raised to the fourth power.
Radiation emitted by the Earth = constant x T4
(with the constant = 5.67 x 10-8
W
/m2/K4)
(Remember that the effective radiating
temperature is expressed in Kelvins!)
We now have all the elements to calculated the effective temperature. We know how much energy the Earth receives and how much radiation is has to emit to get rid of that energy. Using the idea of an energy balance: What comes in = what goes out:
Energy flux
absorbed by the Earth = Radiation emitted by the Earth
239.7 W/m2 = constant x T4
To solve this equation, all we need to do is divide the emitted radiation (239.7 watts per square meter) by the constant (5.67 x 10-8) and take the fourth root of the result. Dividing we obtain 42.3 x 10-8. We'll take the fourth root on a calculator, but to check it's a good idea to estimate the result by taking the square root of 50, which should be just about 7 and taking the square root of 7 which should be around 2.5. The fourth root of 10 to the eighth power is 100. Hence, the answer should be a number around 2.5 x 100 or 250. The calculated result is 255. Remember that all results obtained from the Stefan_Boltzmann Law and other radiation laws are expressed in degrees Kelvin, so this is 255 K (-18 °C, 0 °F):
T = 255 K
The figure below illustrates how we derived this energy balance.

This effective temperature of 255 K is the temperature the Earth's Surface would have if it didn't have an atmosphere. It would be awfully cold! In reality, the Earth's surface temperature is closer to 288 K (15 °C, 59 °F). This difference of 33 K is the magnitude of the greenhouse effect. Before we go into more details about what this greenhouse effect is, let's look at Venus and Mars, our closest neighbours and calculate their effective temperatures.
5) Effective temperatures of Mars and Venus
We express the distance from the Sun in Astronomical units. Venus is 28% closer to the Sun than the Earth, while Mars is 52% further away. The solar flux arriving at Mars and Venus is calculated using the inverse square law (p. 38 in textbook). In the case of Venus:
Flux(Venus)/Flux(Earth) = (Rearth/Rvenus)2
such that Flux(Venus) = 1370 x (1/0.72)2 = 1370 x 1.9 = 2643 W/m2
Venus thus receives almost twice as much solar flux as the Earth.
Mars, which is further way, receives 43% less solar flux than the Earth.
| Venus | Earth | Mars | |
| Distance from Sun (A.U.) | 0.72 | 1 | 1.52 |
| Flux, W/m2 | 2643 | 1370 | 593 |
| Albedo | 0.8 | 0.3 | 0.22 |
| Effective Temperature, K | 220 | 255 | 212 |
| Actual observed Temperature, K | 730 | 288 | 218 |
| Greenhouse Effect, K | 510 | 33 | 5 |
You will notice in the Table above that even though Venus receives more
solar energy than the Earth is, its effective temperature is colder.
This is due to the high albedo on Venus (0.8): 80% of solar radiation is
reflected to space and only 20% is absorbed by the surface (see Figure
3-1 in textbook for a comparison of albedoes of the three planets).
The actual temperature at the suface of Venus is much warmer: 730 K ! The
enormous greenhouse effect of 510 K (=730-220) on Venus is due to high
levels of CO2 in its thick atmosphere. Mars has a much weaker greenhouse
effect because it's atmosphere is much thinner than that of the Earth.
The treatment in the textbook (box on page 43) illustrates the greenhouse
effect by assuming an isothermal atmosphere-- (an atmosphere that is
all at the same temperature) that is perfectly transparent to solar
radiation, but acts like a blackbody in the infrared part of the
electromagnetic spectrum, where the planet emits radiation. It
absorbs all the radiation emitted from the surface of the planet, and
re-emits it: half in the upward direction to space, and half in the
downward direction, back to the surface of the planet. The problem
is
solved by means of simultaneous equations: one is the radiation (or
energy) balance for the surface of the planet and one is for the radiation
balance of the atmosphere. Here is one alternative approach, which
doesn't require solving simultaneous equations.
A simple approach
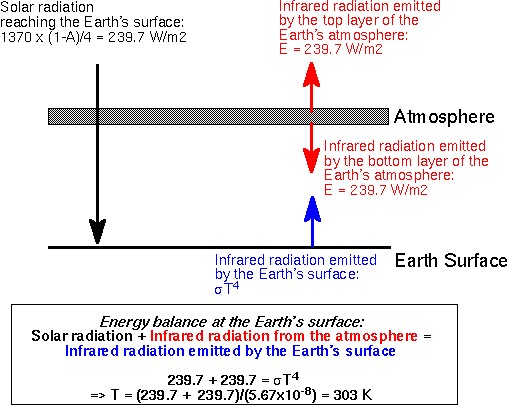
We can get the above results directly by recognizing that the top
layer of the atmosphere must emit 239.7 W/m2 of infrared radiation
to space (same amount of solar radiation that enters the atmosphere:
what goes in must go out). The bottom layer of the atmosphere
will emit an equal amount downward to the surface of the planet.
Hence, for thermal equilibrium, the surface of the planet must emit
enough radiation to balance not only the amount it receives from the
sun (239.7 W/m2), but also what it receives in the form of downward
infrared radiation from the atmosphere 239.7 W/m2). Hence, its emission
must match 239.7+239.7 = 479.4 W/m2. Applying the Stefan-Boltzmann
law: constant x T 4 = 479.4 W/m2. We thus calculate
T = 303 K.
The figure below illustrates this calculation. Contrast
it to the figure
above where we assumed no atmosphere, and you will see where
the greenhouse effect comes in.
The effective temperature we calculate in this manner is much warmer than the actual temperature of the Earth (288 K), because we made a number of simplifying assumptions.
Limitations of this calculation
1) It's assumed that the atmosphere is isothermal. The layer of the
real atmosphere that's most important in terms of the greenhouse
effect is the troposphere, where temperature decreases with height.
Because of this height dependence, the real atmosphere emits more
radiation in the downward direction than in the upward direction (88
units vs. 70 units in Fig. 3-19).
2) It's assumed that the atmosphere absorbs all the outgoing
radiation at all wavelengths in the infrared part of the
electromagnetic spectrum. In reality, the absorption of radiation by
the atmosphere is highly wavelength dependent. At some wavelengths
there's very little absorption and the radiation emitted by the
earth's surface escapes to space, while at other wavelengths it gets
absorbed, reemitted, absorbed and reemitted many times before it
finally escapes. To carry out this calculation accurately it has to
be done wavelength-by wavelength... to capture the fine scale detail
in the spectrum requires literally thousands of calculations
analogous to the one we did in class.
3) Radiative transfer isn't the only process by which energy escapes
from the earth's surface. Conduction of heat and evaporation of water
transfer about twice as much energy from the earth's surface to the
atmosphere as the net upward flux of infrared radiation from the
radiation does. If the temperature distribution on earth were
determined only by radiative transfer (as in this example) the Earth
would be so hot as to be uninhabitable. In this sense the true
'greenhouse effect' on Earth is much larger than the 33 K difference
between the observed surface temperature (288 K) and the effective
radiating temperature (255 K) ascribed to it in your text.
Sample exercises:
(a) Inverse square law
Take two planets, planet A and planet B. Planet B is at 10 times
the
distance from the Sun as planet A. We know the solar flux at
A is
2000 W/m2. What is the flux reaching planet B?
Based on the inverse square law, we have the following relationship
between the fluxes arriving at both planets:
Where Fa and Fb are the solar fluxes arriving at planets A and B, and
Da and Db are the respective distances of these planets from their sun.
We are given the following information:
Fa = 2000 W/m2 and Db =10 x Da
so we can write:
Fb = Fa * (Da/Db)2 = 2000 * (Da/(10 x Da))2 =
2000 x (1/10)2 = 2000 x 1/100 = 20 W/m2
We thus find that the flux arriving at planet B is 120 W/m2 (100 times less than the flux arriving at planet A).
(b) Planetary energy balance and effective radiating temperature
We calculated the effective radiating temperature for Earth in class,
as summarized in the above notes. Let's do the same for Mars. Here
is the information we have: the albedo on Mars is A = 0.22, and the solar
flux reaching Mars is equal to 593 W/m2.
Based on the planetary energy balance applied to Mars, the solar radiation
reaching the planet's surface must be equal to the infrared energy emitted
by the planet:
F(1-A)/4 = constant x T4
with F = 593 W/m2, A = 0.22, constant = 5.67
x 10-8
W /m2/K4
so we find T4
= F(1-A)/4/constant = 593 x (1-0.22)/4/(5.67
x 10-8) = 20.4 x 10+8
K4
Now let's take the fourth root of 20.4 x 10+8
K4,
we find T = 212 K. The effective radiating temperature of Mars is thus
212 K. The observed temperature on Mars is 218 K, so it's atmosphere
has a small greenhouse effect of 218-212 = 6 K.
Last
Updated:
01/14/2002