Radiation tutorial

CONDUCTION by molecular motions, the dominant mechanism in solids and also important in the upper layers of the atmosphere (above 100 km) where molecules are relatively far apart. 

CONVECTION by fluid motions, the dominant mechanism in the oceans and important in the lower atmosphere.  We'll talk about it next week. 

RADIATION consisting of electromagnetic waves traveling at the speed of light: the only mechanism capable of transferring energy through a vacuum (e.g., between the sun and the rest of the universe). 

The units of energy transfer are energy per unit time per unit area. Energy per unit time is also called 'power' and has the unit watts (abbreviated by W).  Hence the rate of energy transfer (e.g., by radiation) is expressed in watts per square meter.  We call this the 'flux' of radiation.  The flux of solar radiation incident on a flat horizontal surface when the sun is directly overhead and the sunlight is undepleted by the atmosphere is 1370 watts per square meter.  1370 watts is roughly equivalent to the electrical power consumed by a hair dryer. 
 

2) The Electromagnetic Spectrum

Radiation comes in a spectrum  (continuous range) of wavelengths, all traveling at the speed of light.  The longer the wavelength of the radiation, the longer it takes a wave to pass a fixed point.  The number of waves that pass a fixed point in a fixed amount of time like a second is called the 'frequency' of the radiation.  Hence, wavelength and frequency are inversely proportional: the longer the wavelength the lower the frequency and vice versa.  Wavelength is expressed in micrometers (often referred to as microns for short, and corresponds to a millionth of a meter) for radiation with short wavelengths and centimeters or even meters for radiation with very long wavelengths 

Names for ranges of the electromagnetic spectrum (in order of increasing wavelength): 

X-RAY- (< 0.01 microns) passes through living tissue, lethal in high doses 
ULTRAVIOLET (UV)- capable of causing sunburn and skin cancer 
VISIBLE- (0.3-0.7 microns)  the narrow range that human eyes are sensitive to 
INFRARED (IR) (0.7-100 microns) important for energy emitted by planets 
MICROWAVE- (beyond 100 microns) carry radio and television signals 

Of all the ranges, x-rays have the highest frequencies, radio waves the lowest. 

3) Radiation as packets of energy

Radiation can also be thought of as consisting of tiny packets of energy called photons.  The more energy in a packet, the more powerful its effects when it collides with matter.  The energy 
carried by photons is inversely proportional to their wavelength. 

Absorbed radiation, regardless of its wavelength produces heating.  If the frequency of the radiation is higher than some threshold, it can facilitate 'photochemical reactions' as well.  For example, the familiar photosynthesis reaction in which plants make chlorophyll requires visible radiation.  More energetic radiation (lower wavelength) can break molecules apart: a process referred to as 'photo-dissociation'.  For example radiation with wavelengths shorter than 0.31 microns (in the UV, just beyond the visible) can break up ozone (O₃) molecules into O atoms and O₂ molecules.  O₂ molecules are more tightly bound together than O₃ molecules so it takes more energy to split them-- the threshold wavelength for photo-dissociation of O₂ is 0.24 microns.  X-rays carry enough energy to strip electrons off atoms, thereby creating electrically charged particles or ions.  This process, referred to as 'photo-ionization', is important at levels of the earth's atmosphere above 60 km (called the ionosphere). 
 

4) Emitted radiation: the Stefan-Boltzmann law

All matter emits radiation at all wavelengths. The maximum amount of radiation that a body can emit, summed over all wavelengths, is proportional to its temperature (expressed in degrees Kelvin) raised to the fourth power.  This relationship is the so called Stefan-Boltzmann law, and is expressed as: 

                     Emitted radiation = constant x T⁴

with constant = 5.67 10^-8 W/m²/K⁴

A body that emits the maximum possible amount of radiation, given its temperature (i.e., the amount prescribed by the Stefan-Boltzmann law) is called a 'blackbody'.  Hence, if we know the flux of radiation emitted by a body, we can use the Stefan-Boltzmann law to calculate the temperature a black body would have to be at in order to emit the equivalent amount of radiation.  The temperature calculated in this manner is known as the 'effective radiating temperature' or the 'equivalent blackbody temperature'.  The radiometer (or 'infrared thermometer') demonstrated in class exploits this principle--- based on the Stefan-Boltzmann law, the radiation scale in its digital circuitry is replaced by a temperature scale. 
 

5) Emitted Radiation: Wien's Law

The wavelength at which the emission from a body is strongest is inversely proportional to its absolute temperature-- that is, the higher its temperature, the shorter the wavelength at which it emits radiation most strongly. This relationship is referred to in the text as Wien's law. 

Bodies the temperature of planets (i.e., hundreds of degrees K) emit virtually all their radiation in the infrared range (around 10 microns).  The 'photosphere' of the sun (the layer from which the sun emits ~99% of its radiation) has a temperature of ~6000 K.  Most of its radiation is in the visible and 'near infrared' parts of the spectrum between 0.3 and 2 microns.  The thin ionized gases in the sun's corona are much hotter than the photosphere.  They're responsible for the x-rays emitted by the sun. Fortunately for us, these gases are so thin that they don't emit very much radiation. 

6) Absorption spectra of gases

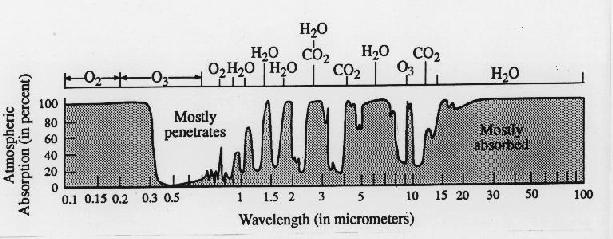
Not all materials behave as blackbodies.  It was demonstrated in class that  ice emits less radiation than a blackbody-- that's why the radiometer gave a reading of -3 C instead of 0 C for the temperature of the ice.  A thin layer of a gas also behaves in a manner different from a black body.  Instead of absorbing all the radiation incident on it and emitting its own radiation almost as a blackbody, it absorbs and emits radiation in narrow ranges of wavelengths referred to as absorption bands.  At wavelengths of the electromagnetic spectrum that lie in between between their absorption bands, these layers of gas are transparent.  Each kind of gas molecule has its own characteristic 'absorption spectrum'.  Gases like ozone (O₃) water vapor (H₂O) and carbon dioxide (CO₂), whose molecules are comprised of three or more atoms, have more and stronger absorption bands in the infrared part of the spectrum than N₂ and O₂ have. 

Figure 3-13 in the text shows the absorption spectrum (the infrared part only) for the Earth's atmosphere.  The figure below extends this graph down to wavelengths 
in the visible and ultraviolet.  The important absorption bands in the spectrum are labeled.  Most of the radiation emitted by the earth's surface in the the narrow 'window region' centered near 10 microns is able to escape directly to space, without being absorbed on its way through the atmosphere. In contrast, radiation at the wavelength of the major absorption bands will be absorbed and emitted many times on its way through the atmosphere. The earth's atmosphere is also nearly transparent to radiation in the visible and near infrared range of the spectrum-- i.e., the wavelengths of incoming solar radiation.  Hence it lets most of the solar radiation in, but blocks most of the outgoing infrared radiation emitted by the earth's surface.  Note that ultraviolet radiation which are harmful to human health are almost entirely absorbed by oxygen
and ozone (O₃) in the atmosphere.

 

 Last Updated:
10/08/2001